The continuous compound interest formula is a mathematical tool used in finance and economics. Unlike traditional compound interest methods, which calculate interest at predetermined intervals, continuous compounding assumes that interest is being added an infinite number of times per year. This approach provides a precise model for scenarios involving constant growth, and is particularly valuable in theoretical finance, investment analysis, bond pricing and financial engineering. Understanding when and why to use the continuous compounding formula can offer deeper insights into the maximum potential growth of investments and other financial processes.
Whether you’re looking to put together an investment portfolio or plan for retirement, a financial advisor can help with a range of investing questions and planning needs.
The Continuous Compound Interest Formula
The continuous compound interest formula calculates interest, assuming that it is being compounded an infinite number of times per year. This method results in the highest possible amount of interest that can be earned over a given period of time.
The formula for continuous compounding is:
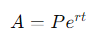
In the formula:
- A is the future value of the investment or loan, including interest.
- P is the principal investment amount (the initial deposit or loan amount).
- e is the base of the natural logarithm, approximately equal to 2.71828.
- r is the annual interest rate (in decimal format).
- t is the time the money is invested or borrowed for (in years).
Example of the Continuous Compound Interest Formula
Assuming an initial investment of $1,000 at an annual interest rate of 5% for 5 years, using the continuous compounding formula, the calculation would be:
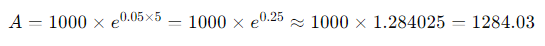
After 5 years, with continuous compounding, the investment would grow to approximately $1,284.03. Continuous compounding can provide a slight edge over other compounding methods, especially for long-term investments.
Continuous Compounding Interest Vs. Other Types of Compounding Interest

The defining feature that sets continuous compounding apart is how often the interest is compounded. In traditional compounding methods, interest can be compounded annually, semi-annually, quarterly, monthly, or daily. Each method of compounding interest results in different amounts of interest accrued over time:
- Annual compounding: Interest is added once per year.
- Semi-annual compounding: Interest is added twice per year.
- Quarterly compounding: Interest is added four times per year.
- Monthly compounding: Interest is added twelve times per year.
- Daily compounding: Interest is added 365 times per year.
In contrast, continuous compounding assumes that interest is being added an infinite number of times per year. And because continuous compounding assumes an infinite number of compounding periods, its calculation results in slightly higher interest accumulation compared to even daily compounding. This is because with each additional compounding period, the interest is being calculated on an increasingly larger amount of principal plus all of the previously earned interest.
Practical Applications
Continuous compounding is a theoretical concept that is used primarily in mathematical finance and certain advanced investment strategies. In practical terms, most financial institutions use daily, monthly, or quarterly compounding. It’s easier to implement, and more easily understood by clients. However, understanding continuous compounding can provide insight into the maximum potential growth of an investment under ideal conditions.
Here are six other situations in which the continuous compounding interest formula is used:
- Theoretical finance and mathematics: Continuous compounding is often used in theoretical finance and mathematics to model scenarios where compounding occurs constantly. It serves as a useful approximation for understanding the upper limits of investment growth and for simplifying complex mathematical calculations.
- Investment and portfolio analysis: In investment and portfolio analysis, continuous compounding is used to compare different investment opportunities. It provides a benchmark for evaluating the potential returns of various financial instruments, helping investors to make more informed decisions about where to allocate their resources.
- Bond pricing: Continuous compounding is frequently used in the pricing of zero-coupon bonds and other financial derivatives. The present and future value of these instruments are often calculated using continuous compounding to account for the constant accrual of interest over time.
- Exponential growth models: In scenarios involving exponential growth, such as population growth, radioactive decay, and certain economic models, continuous compounding provides a precise way to represent the growth rate. The continuous compounding formula can be adapted to describe these processes accurately.
- Financial engineering: In financial engineering, continuous compounding is used to model the growth of assets and liabilities. It’s particularly useful when it comes to valuing financial derivatives, risk management, and the development of new financial products. The continuous compounding formula allows for a more straightforward analysis of complex financial problems.
- Education and learning: Continuous compounding is also used as an educational tool to teach the concepts of limits and exponential functions in calculus and financial mathematics courses. By understanding continuous compounding, students gain insights into more advanced topics in finance and economics.
Bottom Line

The continuous compounding interest formula can provide a precise model for understanding and maximizing investment growth. Its applications extend from theoretical finance to practical investment analysis, bond pricing and financial engineering. By leveraging this formula, investors and financial professionals can gain deeper insights into the potential returns of various financial instruments and effectively model exponential growth scenarios.
Investment Tips
- A financial advisor can help you create a personalized investment plan for your goals and needs. Finding a financial advisor doesn’t have to be hard. SmartAsset’s free tool matches you with up to three vetted financial advisors who serve your area, and you can have a free introductory call with your advisor matches to decide which one you feel is right for you. If you’re ready to find an advisor who can help you achieve your financial goals, get started now.
- If you want to create an investment portfolio based on your risk tolerance, SmartAsset’s free asset allocation calculator can help you select a profile that aligns with your preferences.
Photo credit: ©iStock.com/nespix, ©iStock.com/BongkarnThanyakij, ©iStock.com/Kobus Louw
